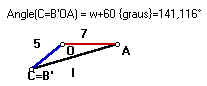Fugiremos um pouco de alguns detalhes matemáticos muitas vezes até convenientes no dia-a-dia, mas que não farão a menor falta a este texto. A saber:
Trataremos indistintamente AB como o segmento que liga o ponto A ao ponto B ou como a medida deste segmento.
Trataremos de circunferência ou círculo o conjunto de todos os pontos de um plano que estão a uma distância fixa de um ponto fixo (centro). Se necessário, chamaremos de disco os pontos que estão a uma distância menor ou igual à referida distância fixa do referido ponto fixo (centro)
Problema 1
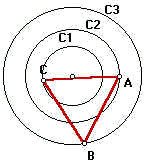
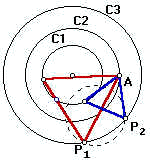
Dados três círculos concêntricos C1, C2, C3 de raios r1>r2>r3. Construa um triângulo equilátero de forma que cada uma das circunferências contenha somente um de seus vértices.
| Normalmente fica mais fácil resolver os problemas de construção pensando de trás para frente. Por exemplo, suponhamos que o problema esteja resolvido (se é que ele pode ser resolvido!). |
|
| Rotacionando a circunferência menor em torno de A por um ângulo de 60o levaremos o ponto C ao encontro de B. Mas vejamos que o ponto B é o ponto onde a circunferência rotacionada encontra a circunferência maior... Isso nos dá uma idéia de como proceder para resolver o problema. |
|
|
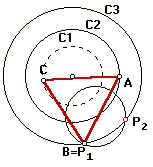
Rotacionemos C1 de 60o em torno de um ponto qualquer A em C2. Notemos que a escolha de A e de C2 é arbitrária (poderíamos muito bem ter escolhido um ponto em C3 ou em C1). Vejamos que a circunferência menor toca a maior em dois pontos P1 e P2. Isso indica que o problema tem duas soluções. Da mesma forma, as circunferências poderiam ter se tocado em um único ponto ou em nenhum ponto (caso em que o problema não teria solução).
|
|
| Mas como fazer para achar o triângulo?
Ora, uma vez que conhecemos um de seus lados (no caso, qualquer um dos segmentos AP1 ou AP2). Basta realizarmos a operação inversa dos pontos P1 e P2 (rotação de 60o no sentido horário com centro em A).As duas soluções estão na figura em azul e vermelho.
Resta agora a intrigante pergunta: estas soluções são as únicas?
Percebamos que onde quer que se encontre o vértice A sobre o círculo C2 sempre poderemos usar o raciocínio da rotação para achar os outros pontos B e C. Ora, mas sempre que fizermos a rotação, neste caso, só acharemos dois pontos de contato, logo, dois possíveis lados para o triângulo.
Suponhamos que você tenha então achado um triângulo por um outro método. Um de seus vértices deverá estar no círculo C2 (por exigência do enunciado), Logo poderemos repetir o raciocínio da rotação de C1 para achar os outros vértices. Mas aquele raciocínio para este problema só conduz a duas medidas possíveis para o lado do triângulo equilátero. Logo, o triângulo que você achou é um desses que achamos, rotacionado.
|
|
|
| Problema 2
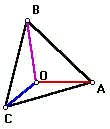
Considere um ponto fixo O. Determine o lado do triângulo equilátero cujos vértices estão a distâncias iguais a 5, 7 e 8 unidades deste ponto.
|
Novamente vamos considerar o problema resolvido.
Para não tumultuar o desenho, não atribuímos nomes aos segmentos OC, OA e OB que valem respectivamente 5, 7 e 8 unidades.
|
|
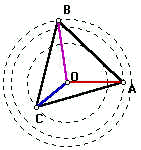
| Perceba que podemos traçar círculos com centro em O que passem por A, B e C. De tal forma a fazer este problema lembrar o anterior. O que fizemos foi rotacionar o círculo menor de 60o. Tentemos fazer o mesmo rotacionando o triângulo ABC e tudo que está dentro de 60o em qualquer sentido. |
|
| Como desejamos saber a medida do lado AC, basta olharmos para o triângulo AOC. Neste triângulo são conhecidos os lados CO, AO e o ângulo AOO'. Para descobrirmos a medida do lado AB do triângulo equilátero, é suficiente descobrir o ângulo COO'. Descobrir este ângulo é trivial, já que conhecemos as medidas dos três lados CO, OO' e CO'.
Segue que:
82=72+52-2.7.5.cos w
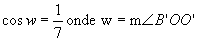
Obviamente fica fácil calcular o sen w.
cos2w +sen2w=1
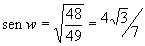
cos(w+60o)=cosw.cos 60o –senw.sen60o
Ou seja,
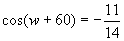
logo, chamando de "l" o lado do triângulo equilátero procurado, teremos:
l2=52+72-2.5.7.(-11/14). Ou seja,
l=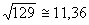 . .
Eis o lado tão cobiçado:11,36 unidades de comprimento.
|
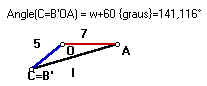
|
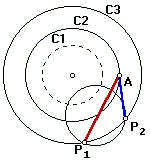
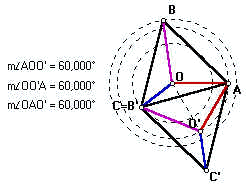
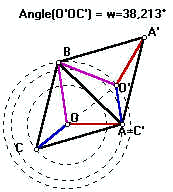
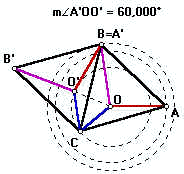
Um aluno um pouco mais curioso poderia indagar: e se utilizássemos como centro de rotação um outro ponto. digamos B ou C. O que aconteceria?
Neste problema, especificamente, você certamente achará ângulos mais agradáveis de se trabalhar se tentar rotacionar em torno de outro ponto. Isso poderá diminuir um pouco o trabalho investido em se achar a solução, mas não muda o resultado.
Ao lado mostramos as duas outras possíveis rotações. Se você se der ao trabalho de fazer as contas verificará que o ângulo que chamamos de w muda de uma para outra.Ao final da conta, o lado achado será fatalmente o mesmo.
|
|
|