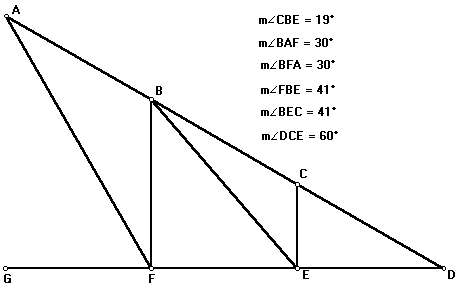Para falar com o prof Demétrius, por favor, clique aqui!
Problema de Estática - Treliça |
|
|
|
| Seccionaremos a figura através dos cortes C1, C2 e C3 e imporemos a cada um dos sistemas as condições usuais de equilíbrio. Se o sistema representar um ponto, teremos que a somatória das forças externas será zero. Se as forças não concorrerem em um único ponto, além da condição anterior, diremos que a somatória dos momentos das forças com relação a um ponto qualquer será zero também. | |
|
|
Corte C1:
DC. sen30o – P = 0 (equilíbrio na vertical) è DC=2P DE+DCcos30o=0 è DE=-1,732P
|
|
|
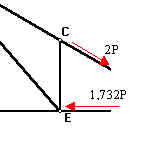
Corte C2:
Somatória das componentes verticais das forças: Somatória das componentes horizontais é zero: Somatória dos momentos com relação ao ponto E vale zero: Logo, CB=2P Substituindo ambos em [2], encontraremos: Isolando o nó "C" vemos que CE=0; |
|
|
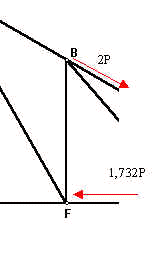
Corte C3:
Note que aplicando as mesmas equações do corte anterior chegaremos às mesmas conclusões: BF=FA=zero
|
|
Na verdade, esta treliça funciona como se BF, CE, AF e BE não existissem. Problemas de treliças normalmente são resolvidos ou pelo método dos nós, ou pelo método dos cortes. Mas a maneira mais rápida de verdade é usar o bom senso para empregar ambos, cada um quando for mais conveniente. |
|