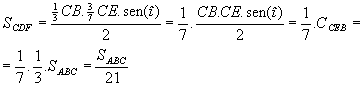Área entre Cevianas e Lados

Área entre cevianas e lados.


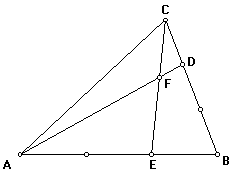
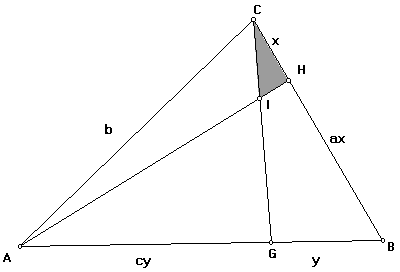
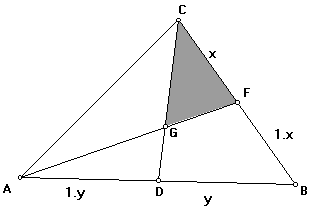
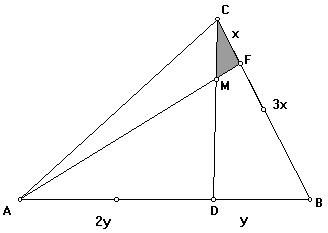
Considere o triângulo ABC onde CD=CB/3 e BE=AB/3. Se a área do triângulo ABC vale 1. Calcule a área do triângulo CDF.
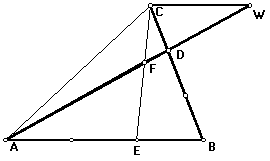
	Prolongando o segmento AD até encontrar a paralela a AB que passa por C teremos uma figura de onde poderemos tirar duas relações de semelhança: Na figura ao lado, a razão de semelhança entre o triângulo CDW e o BDA é ½. Logo: (1) e (2)
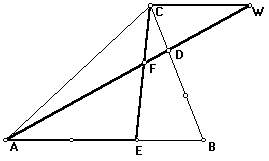
	Na Figura ao lado, a razão de semelhança entre o triângulo CWF e o triângulo EFA é: (3) Donde: (4) e CF=3FE/4 (5)
Usando as igualdades 2 e 4, acharemos que FA=6DF. Como já sabemos, de (5), que CF=3FE/4. Agora fica fácil calcular a área desejada. A área do triângulo CEB é um terço da área do triângulo ABC. Isso é fácil ver porque . Ou seja, como a área é proporcional a dois quaisquer lados e aos ângulo entre eles, se dilatarmos apenas um desses lados, multiplicando-o por k, a área toda fica multiplicada por k. Chamando o ângulo ECB de " î "e percebendo que CF=3CE/7,teremos que: Resposta: 1/21.

GENERALIZANDO...

morgado_a.gif (2838 bytes)

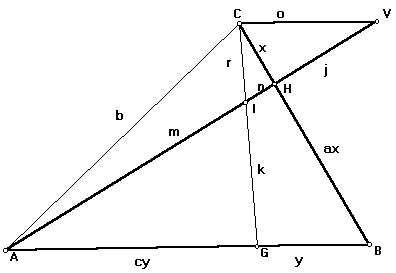
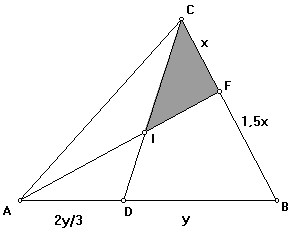
Considere a figura acima. Sabendo que a área do triângulo ABC vale 1, determine a área do triângulo CIH.

Traçando uma paralela a AB passando por C e estendendo o segmento AH, teremos que:

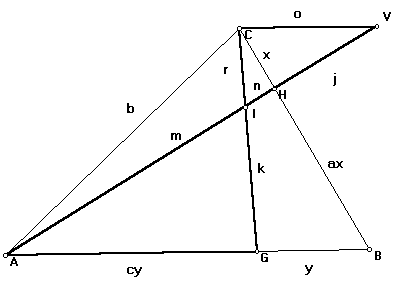
	Os triângulos CHV e BHA são semelhantes e a razão de semelhança do segundo para o primeiro vale "a", ou seja, os lados do triângulo BHA são "a" vezes os respectivos lados homólogos do triângulo CHV. Desta forma, AB=a.o (1) e m+n=aj (2).
	Os triângulos CIV e GIA são semelhantes e a razâo de semelhança do segundo para o primeiro vale Mas, de (1), AB=o.a, o que faz a razão de semelhança ser ac/(c+1). Isto implica que os lados do triângulo AGI são os lados do triângulo CVI multiplicados por ac/c+1. Logo, (3) e (4)
Já sabemos a relação existente entre k e r. Resta saber a relação existente entre m e n. Eliminando j a partir de (2) e (4) encontramos m=n.c.(a+1). Calculando então a área do triângulo CIH... A área do triângulo CGB pode ser calculada dividindo-se a área do triângulo ABC por (c+1) e multiplicando o resultado por 1. Logo, . O triângulo CIH pode ser visto como tendo sindo obtido a partir de CGB multiplicando-se os lados CG e CB respectivamente por e . Logo, Como a área de um triângulo é proporcional a dois quaisquer lados e ao seno do ângulo entre eles, . Alguns exemplos:
*Se as cevianas são medianas...*	Nesta caso, a=1 e c=1, Logo, . Ou seja, a área do triângulo hachurado é 1/6 da área do triângulo ABC.